Orbital Mechanics How Things Works
Orbital Mechanics How Things Works
Gravity & Mechanics
How Orbits Work
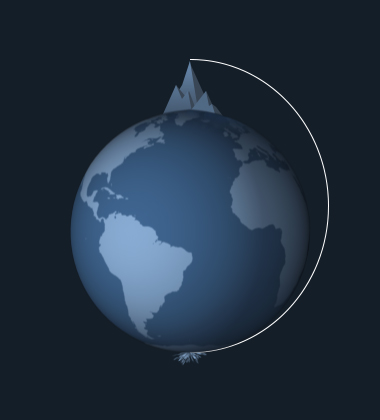
These drawings simplify the physics of orbital mechanics, making it easy to grasp some of the basic concepts. We see Earth with a ridiculously tall mountain rising from it. The mountain, as Isaac Newton first described, has a cannon at its summit.
Of course, in order to make their point, the cartoons on this page ignore lots of facts, such as the impossibility of there being such a high mountain on Earth, the drag exerted by the Earth's atmosphere on the cannonball, and the energy a cannon can impart to a projectile ... not to mention how hard it would be for climbers to carry everything up such a high mountain! Nevertheless, the orbital mechanics they illustrate (in the absence of details like atmosphere) are valid.
When the cannon is fired, the cannonball follows its ballistic arc, falling as a result of Earth's gravity, and of course it hits Earth some distance away from the mountain.
If we pack more gunpowder into the cannon, the next time it's fired, the cannonball goes faster and farther away from the mountain, meanwhile falling to Earth at the same rate as it did before. The result is that it has gone halfway around the cartoon planet before it hits the ground. (You might enjoy the more elaborate animation at Space Place.)
Packing still more gunpowder into the capable cannon, the cannonball goes much faster, and so much farther that it just never has a chance to touch down. All the while it would be falling to Earth at the same rate as it did in the previous cartoons. This time it falls completely around Earth! We can say it has achieved orbit.
That cannonball would skim past the south pole, and climb right back up to the same altitude from which it was fired, just like the cartoon shows. Its orbit is an ellipse.
This is basically how a spacecraft achieves orbit. It gets an initial boost from a rocket, and then simply falls for the rest of its orbital life. Modern spacecraft are more capable than cannonballs, and they have rocket thrusters that permit the occasional adjustment in orbit, as described below. Apart from any such rocket engine burns, they're just falling. Launched in 1958 and long silent, the Vanguard-1 Satellite is still falling around Earth.
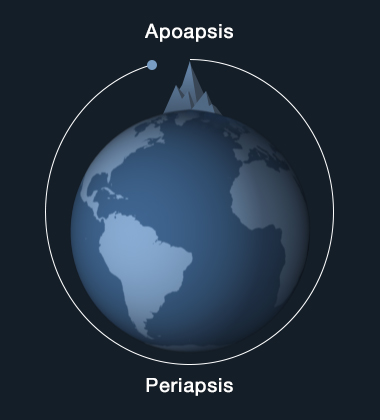
In the third cartoon, you'll see that part of the orbit comes closer to Earth's surface than the rest of it does. This is called the periapsis of the orbit. The mountain represents the highest point in the orbit. That's called the apoapsis. The altitude affects the time an orbit takes, called the orbit period. The period of the space shuttle's orbit, at say 200 kilometers, used to be about 90 minutes. Vanguard-1, by the way, has an orbital period of 134.2 minutes, with its periapsis altitude of 654 km, and apoapsis altitude of 3,969 km.
The Key to Space Flight
Basically all of space flight involves the following concept, whether orbiting a planet or travelling among the planets while orbiting the Sun.
As you watch the third cartoon's animation, imagine that the cannon has been packed with still more gunpowder, sending the cannonball out a little faster. With this extra energy, the cannonball would miss Earth's surface at periapsis by a greater margin, right?
Right. By applying more energy at apoapsis, you have raised the periapsis altitude.
A spacecraft's periapsis altitude can be raised by increasing the spacecraft's energy at apoapsis.
This can be accomplished by firing on-board rocket thrusters when at apoapsis.
And of course, as seen in these cartoons, the opposite is true: if you decrease energy when you're at apoapsis, you'll lower the periapsis altitude. In the cartoon, that's less gunpowder, where the middle graphic shows periapsis low enough to impact the surface. In the next chapter you'll see how this key enables flight from one planet to another.
Now suppose you increase speed when you're at periapsis, by firing an onboard rocket. What would happen to the cannonball in the third cartoon?
Just as you suspect, it will cause the apoapsis altitude to increase. The cannonball would climb to a higher altitude and clear that annoying mountain at apoapsis.
A spacecraft's apoapsis altitude can be raised by increasing the spacecraft's energy at periapsis.
This can be accomplished by firing on-board rocket thrusters when at periapsis.
And its opposite is true, too: decreasing energy at periapsis will lower the apoapsis altitude. Imagine the cannonball skimming through the tops of some trees as it flys through periapsis. This slowing effect would rob energy from the cannonball, and it could not continue to climb to quite as high an apoapsis altitude as before.
In practice, you can remove energy from a spacecraft's orbit at periapsis by firing the onboard rocket thrusters there and using up more propellant, or by intentionally and carefully dipping into the planet's atmosphere to use frictional drag. The latter is called aerobraking, a technique used at Venus and at Mars that conserves rocket propellant.
Orbiting a Real Planet
Isaac Newton's cannonball is really a pretty good analogy. It makes it clear that to get a spacecraft into orbit, you need to raise it up and accelerate it until it is going so fast that as it falls, it falls completely around the planet.
In practical terms, you don't generally want to be less than about 150 kilometers above surface of Earth. At that altitude, the atmosphere is so thin that it doesn't present much frictional drag to slow you down. You need your rocket to speed the spacecraft to the neighborhood of 30,000 km/hr (about 19,000 mph). Once you've done that, your spacecraft will continue falling around Earth. No more propulsion is necessary, except for occasional minor adjustments. It can remain in orbit for months or years before the presence of the thin upper atmosphere causes the orbit to degrade. These same mechanical concepts (but different numbers for altitude and speed) apply whether you're talking about orbiting Earth, Venus, Mars, the Moon, the sun, or anything.
A Periapsis by Any Other Name
Periapsis and apoapsis are generic terms. The prefixes "peri-" and "ap-" are commonly applied to the Greek or Roman names of the bodies which are being orbited. For example, look for perigee and apogee at Earth, perijove and apojove at Jupiter, periselene and apselene or perilune and apolune in lunar orbit, pericrone and apocrone if you're orbiting Saturn, and perihelion and aphelion if you're orbiting the sun, and so on.
Freefall
If you ride along with an orbiting spacecraft, you feel as if you are falling, as in fact you are. The condition is properly called free fall. You find yourself falling at the same rate as the spacecraft, which would appear to be floating there (falling) beside you, or around you if you're aboard the International Space Station. You'd just never hit the ground.
Notice that an orbiting spacecraft has not escaped Earth's gravity, which is very much present -- it is giving the mass the centripetal acceleration it needs to stay in orbit. It just happens to be balanced out by the speed that the rocket provided when it placed the spacecraft in orbit. Yes, gravity is a little weaker on orbit, simply because you're farther from Earth's center, but it's mostly there. So terms like "weightless" and "micro gravity" have to be taken with a grain of salt... gravity is still dominant, but some of its familiar effects are not apparent on orbit.
Orbital Mechanics 101
- October 24, 2020
In 1687, Isaac Newton published “A Treatise of the System of the World”, which formed the foundation of classical mechanics. In a chapter of this work Newton visualises a cannon on top of a very high mountain. If there were no forces of gravitation or air resistance, the cannonball should follow a straight line away from Earth, in the direction that it was fired. If a gravitational force acts on the cannonball, it will follow a different path depending on its initial velocity. If the speed was the orbital speed at that altitude, it would go on circling around the Earth along a fixed circular orbit, just like the Moon. This visualisation is key for understanding orbital mechanics.
Figure 1. Image from page 6 from Newton’s Philosophiæ Naturalis Principia Mathematica Volume 3.
There are dozens of different kinds of orbits that are used for multiple purposes, telecommunications, science, technology demonstrations, remote sensing, but in this article, we will explain the most common application orbits.
Figure 2. Representation of multiple orbits.
However, before getting to learn about different orbits we shall understand first some basic parameters and artificial constructions developed to visualise and comprehend the space bodies motion.
The first thing to understand is that the orbits are not circular, they are elliptical, an ellipse is a closed plane curve surrounding two focal points, and for all points on the curve, the sum of the two distances to the focal points is a constant.
Figure 3. Condition for all points of the ellipse.
The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0, when it is a circle and the two foci are at the same point, to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola, not an open orbit). To calculate the eccentricity as the ratio between the distance from the centre to the focus and the distance between the co-vertex to the focus, the elements can be found in the following image to visualise it better. The value of the eccentricity of an orbit could be bigger than one but it would no longer be a closed orbit, it would be a hyperbola, but we are going to focus in this article in elliptical orbits.
Figure 4. Ellipse notations.
Equation 1. Mathematical definition of eccentricity.
In the following image we can see several orbits around Earth with different eccentricities. As it is appreciated the smaller the eccentricity the most similar the orbit is to a circle. As a matter of fact, some of the space bodies of the Solar System have very small eccentricities and their orbits are almost circular, this data can be shown in table 1.
Figure 5. Orbits with different eccentricities.
Table 1. Eccentricity of space bodies in the Solar System.
The central body of the system is always in one of the foci of the ellipse, the Sun for the Solar System and Earth for satellite orbits. The periapsis is how it is called the point in the orbit where the distance between the bodies is minimal. And the apoapsis is the point in the orbit where the distance between the bodies is maximum. When talking about Earth these points are called perigee and apogee.
Figure 6. Periapsis and apoapsis locations.
The mean value of the periapsis and apoapsis, also the semisum, results in the value of the semi-major axis, a, which is half the longitude of the distance of the biggest axis of the ellipse.
Figure 7. Semimajor axis.
When defining an orbit, apart from distances there are also angles involved. We will go through some of the most relevant and helpful to understand. But firstly, we shall define the references for defining angles, for such thing we create artificial geometrical constructions to visualise them.
The first of these constructions is the Equatorial plane, which, as the name suggests, contains the Equator of Earth. The second plane is the orbit plane, which, as the name suggests, contains the orbit. The angle between those two planes is the inclination angle, it varies between 0º and 180º. When the inclination angle is less than 90º the orbit is called prograde or direct, when the inclination angle is greater than 90º the orbit is called retrograde or indirect, and when the inclination angle is exactly 90º and the orbit goes over the poles the orbit is called polar orbit.
Figure 8. Inclination angle.
The next angle is the Right Ascension of the Ascending Node (RAAN), Ω, which is the equivalent of terrestrial longitude in space. RAAN is measured from the Sun at the March equinox, which is the place on the celestial sphere where the Sun crosses the celestial Equator from South to North at the Spring equinox and there are the same amount of light hours and darkness at the Equator.
Figure 9. Seasonal configuration of Earth and Sun.
RAAN is measured continuously in a full circle from that alignment of Earth and Sun in space, that equinox, the measurement increasing towards the East.
Figure 10. Concept of Right Ascension of the Ascending Node (RAAN).
Another relevant angle is the argument of the perigee, ω, is the angle from the body’s ascending node to its periapsis, measured in the direction of motion. An argument of perigee of 0° means that the orbiting body will be at its closest approach to the central body at the same moment that it crosses the plane of reference from South to North.
Figure 11. Concept of Argument of the Perigee.
After studying the most relevant angles we will see the most relevant orbits, the ones that are most used. The first three that we are going to see are Low Earth Orbit (LEO), Medium Earth Orbit (MEO) and Geosynchronous Earth Orbit (GEO), being the parameter that differentiates them their distance from the surface of Earth, their altitude. But that will be explained in the next article.
Figure 12. Most used orbits.
Comments
Post a Comment